Deep Learning Research
Last updated: July 2018
Deep neural networks (DNNs) have proven themselves capable of learning to solve a wide range of difficult tasks. However, the solutions these networks use to solve these tasks remain poorly understood, earning DNNs their reputation as black boxes. Furthermore, our lack of understanding of DNN solutions means we also lack a clear understanding of their bottlenecks, making intelligent, scientifically motivated improvements extremely challenging. As a result, our field has largely improved DNNs through trial and error, distributed across hundreds, if not thousands, of groups across the world. This situation is akin to trying to build a clock without understanding how individual gears fit together.
Using rigorous, scientific methods (often inspired by neuroscience), my goal is to better understand the solutions used by DNNs and, perhaps most critically, their bottlenecks, so that we can intelligently design machine learning systems.
Generalization
Ultimately, our networks are only useful if they make accurate predictions in situations they've never seen before. As such, training networks which generalize is absolutely critical. However, the properties of learned network solutions which lead networks to generalize remain poorly understood.
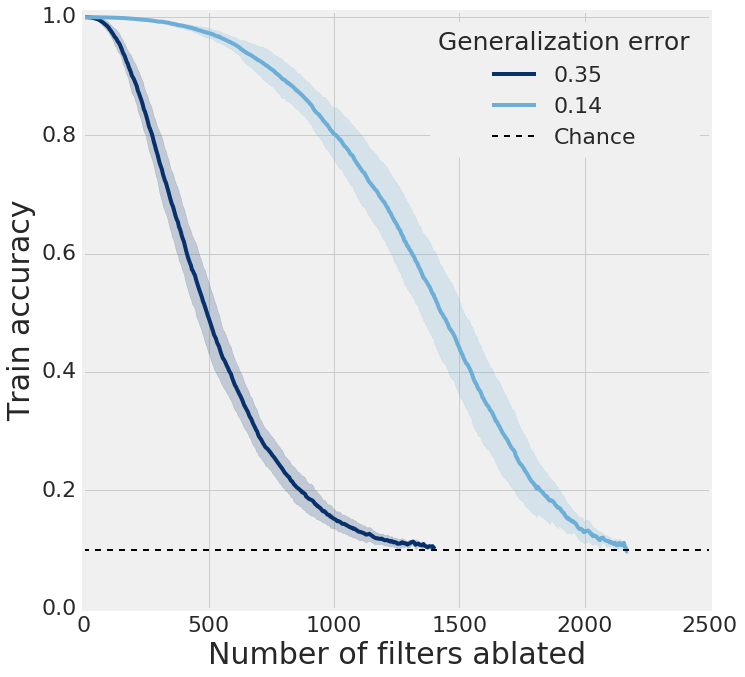
In one recent study, we used neuron ablation to demonstrate that networks which generalize well are much more robust to perturbation of their hidden state than those which generalize poorly in a variety of contexts. We also showed that, though it may seem counterintuitive, dropout does not in fact regularize for this, yet batch normalization does.
We recently extended this work, using Canonical Correlation Analysis (CCA) to measure the similarity of networks with different random initializations. We found that networks which generalize converge to more similar solutions than those which memorize, and that wider networks converge to more similar solutions than narrow networks. Moreover, we found that across these contexts, the similarity of converged solutions was a strong predictor of test accuracy, despite the fact that it was computed based only on the training set.
Representation learning and abstraction
Building intelligent systems will likely require teaching our models to build abstract representations of their environment. Systems which are capable of abstract reasoning will likely generalize better, not only to unseen similar situations, but to situations which overlap only in subtle, high-level ways. However, in order to optimize for abstract reasoning ability, we have to be able to measure it, both behaviorally and representationally.
To measure abstract reasoning behaviorally, we developed a task inspired by Raven's Progressive Matrices which allows for precisely controlled overlap between the train and test distributions. This enables us to measure which concepts in the task neural networks have abstracted and which concepts they haven't. While neural networks can currently perform some abstraction tasks well (like interpolation), the majority still remain well beyond their current capabilities.
We recently extended this work, finding that while architecture choice can influence generalization performance, choosing data for training such that plausible options most highlight the relevant concepts is critical. By choosing distractors in this manner, we were able to significantly improve generalization to novel test distributions.
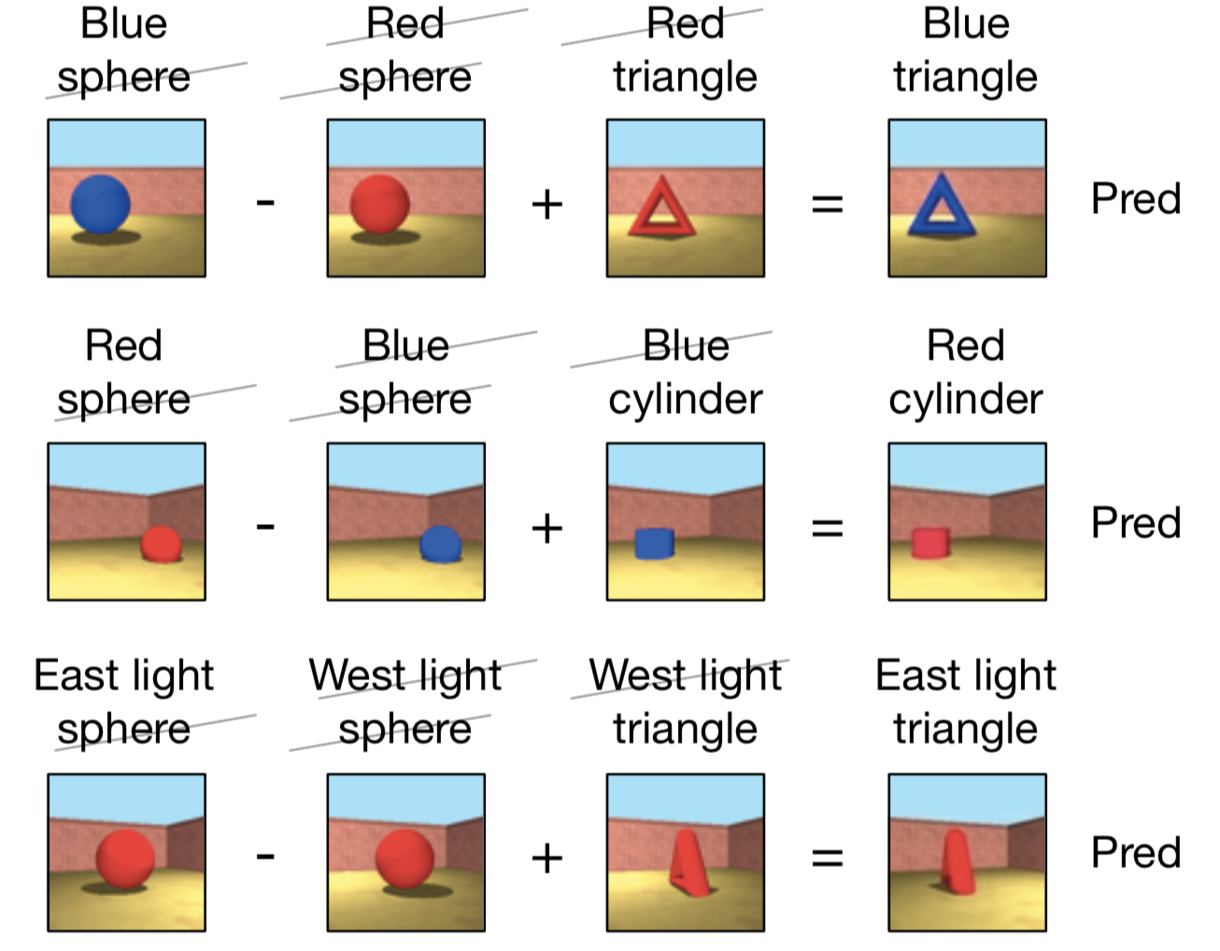
To measure abstract reasoning representationally, we developed several new approaches in an investigation of Generative Query Networks (GQNs) to show that GQN representations were factorized with respect to various primitives, such as color and shape. As a clear example of analysis informing model design, we initially found that the GQN's representation was highly context-dependent, and used insights from this analysis to inform an intelligent design change which improved model performance.
Generic understanding
The field of deep learning is full of assumptions and intuitions which have never been empirically tested. This has likely led to substantial research debt, as researchers attempt to build on reasoning which is often flawed. Testing these intuitions should enable faster iteration and progress, allowing us to iterate based on concepts we know are true, rather than concepts we just think are probably true.
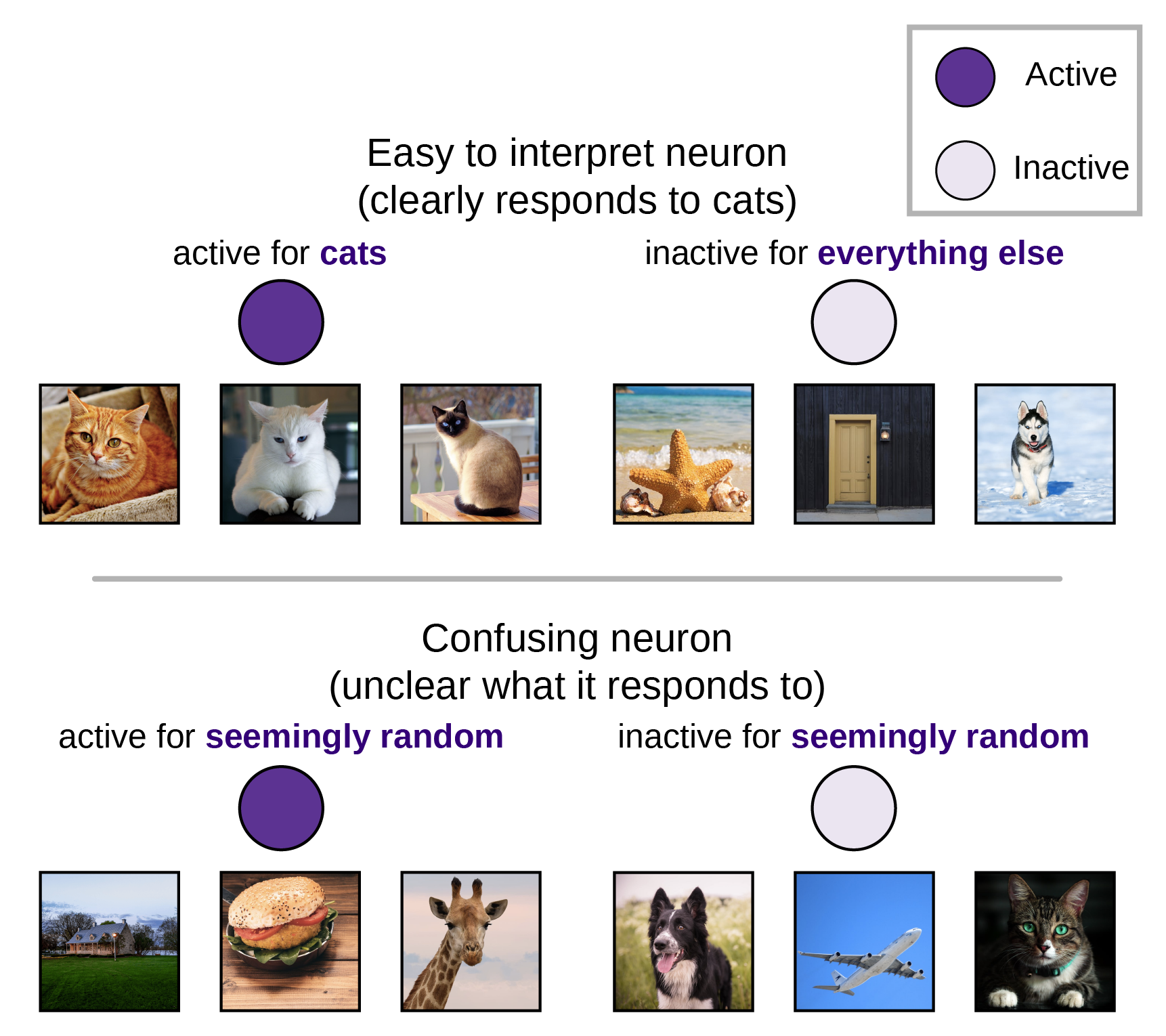
Much of the focus on understanding neural networks, both in deep learning and in neuroscience has focused on the role of single units, based on the assumption that single units which are selective for task features are more important to the computation than those which exhibit more confusing response patterns. However, this assumption had remained largely untested until we recently evaluated the relationship between selectivity and unit importance. Surprisingly, we found that, for image classification tasks, selective units were no more important than non-selective units.
For years, much of the success of convolutional neural networks (CNNs), especially with respect to deformation stability, had largely been attributed to interleaved pooling layers. However, recent CNNs have nearly abandoned pooling altogether. By measuring deformation stability in CNNs with and without pooling, we found that the deformation stability conferred by pooling is actually too strong, and that networks converge to the same layerwise pattern of deformation stability regardless of whether or not pooling is present. Finally, we demonstrated that deformation stability is largely determined by filter smoothness rather than pooling.